Finding closest locations with GKRTree in Swift
In one of my iOS apps, I have recently faced a problem where I had to efficiently look up locations that are geographically close to a specified point. As the naive approach, including computing a distance between dozens of point pairs, seem not so efficient to me - I made a little research and gave a try to Apple-provided R-tree implementation from GameKit.
This story is a quick dive into R-tree basics as well as features a short Apple-provided GKRTree usage example.
R-tree basics
R-tree is a data structure that has a wide application for indexing spatial data. The concept was first proposed by Antonin Guttman in 1984. The key idea behind R-tree is grouping nearby objects and representing them with their minimum bounding rectangles or boxes. The minimum bounding rectangle, often referred to as MBR, is the smallest rectangle that contains a given group of objects. The MBRs of higher-level group MBRs of child nodes. That makes searches in the tree efficient as the query that does not intersect the bounding rectangle on a higher level also cannot intersect any of the contained objects MBRs. That makes filtering out non-matching elements faster.
To have a better image of how the data are structured, let's have a short look at that diagram from Wikipedia. We can see top-level, black marked regions that cover the biggest parts of the surface and contain smaller blue areas. We can observe that when searching for an element lying inside R15 box we can filter out all R1 children in just one comparison significantly reducing the amount of computation needed for a search operation.
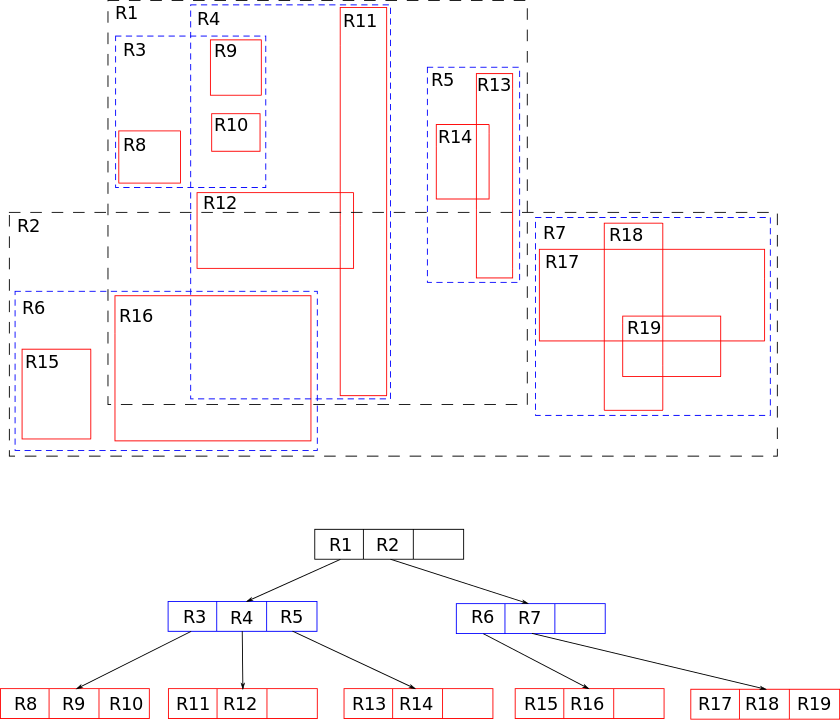
R-tree is also a balanced search tree, which means that all leaves are on the same level. Additionally, that structure is also optimized for disk storage, so it found wide application in the database field.
R-trees can be useful for many tasks:
- Finding POI's that are within a certain distance from a given location
- Deciding which game objects are close enough to trigger interactions
- Searching closest nodes in the coordinates grid
- And many more...
R-tree in Swift
GKRTree is an implementation of R-tree concept provided by Apple in GameKit. As I am rather a type of person that relies on deeply-tested and battle-proven implementations, so rather than implementing one myself, I gave it a try in my use case.
Let's assume that our data are locations represented by the following class. It's required for an object being GKRTree element to be NSObject's subclasses.
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
let name: String
let x: Float
let y: Float
init(name: String, x: Float, y: Float) {
self.name = name
self.x = x
self.y = y
super.init()
}
}
For creating an instance of GKRTree it's needed to specify maximum capacity. Let's then specify a couple of Location instances and create a GKRTree object.
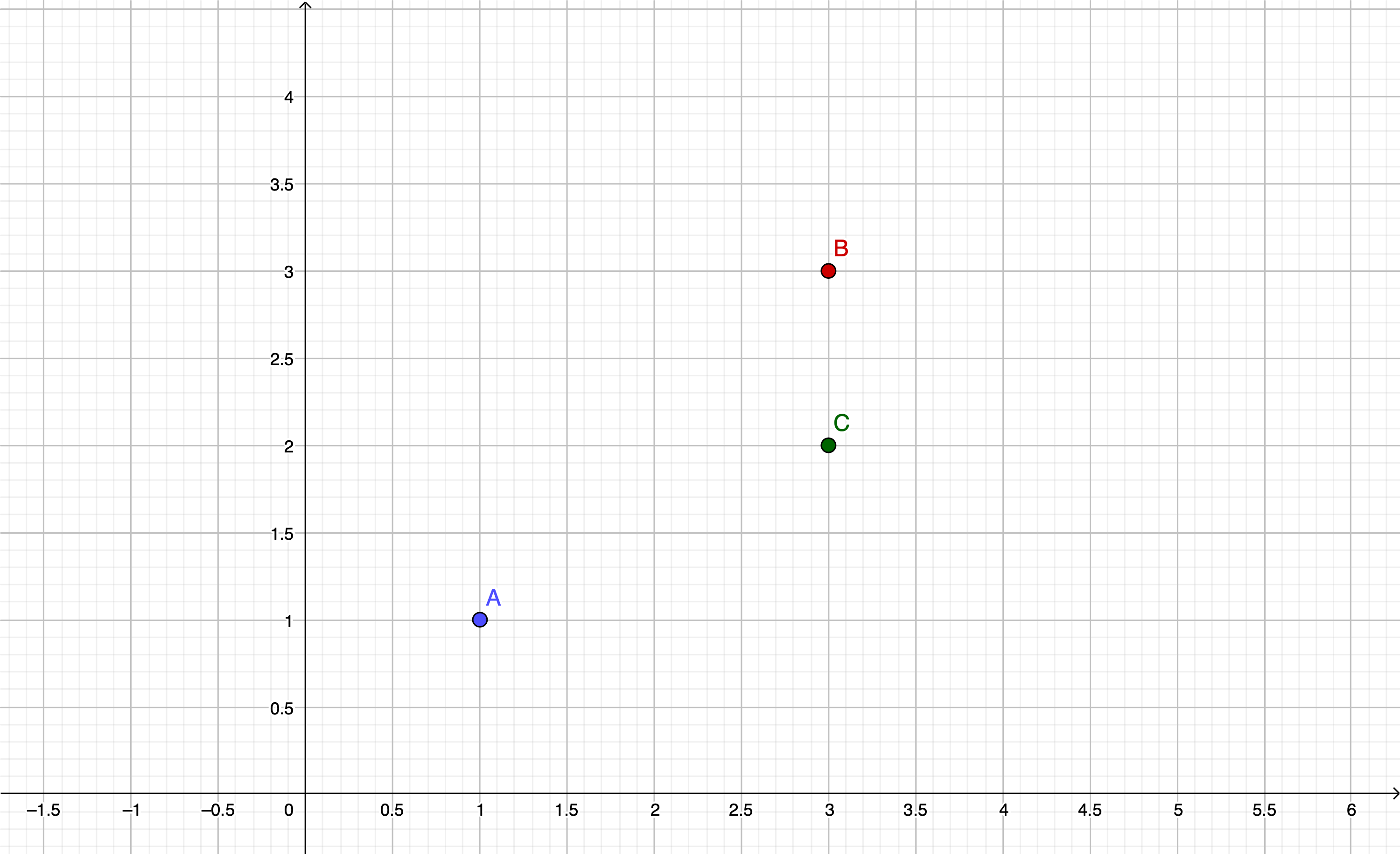
let sampleLocations = [
SomeLocation(name: "A", x: 1.0, y: 1.0),
SomeLocation(name: "B", x: 3.0, y: 3.0),
SomeLocation(name: "C", x: 3.0, y: 2.0)
]
let rTree = GKRTree(maxNumberOfChildren: sampleLocations.count)
Our points may be drawn using the below diagram, which may be helpful to visualize the spatial relationships between them.
Once we have an R-tree instance and elements created, it's time to put them into the actual structure. The API for that looks as follow
func addElement(_ element: ElementType,
boundingRectMin: vector_float2,
boundingRectMax: vector_float2,
splitStrategy: GKRTreeSplitStrategy)
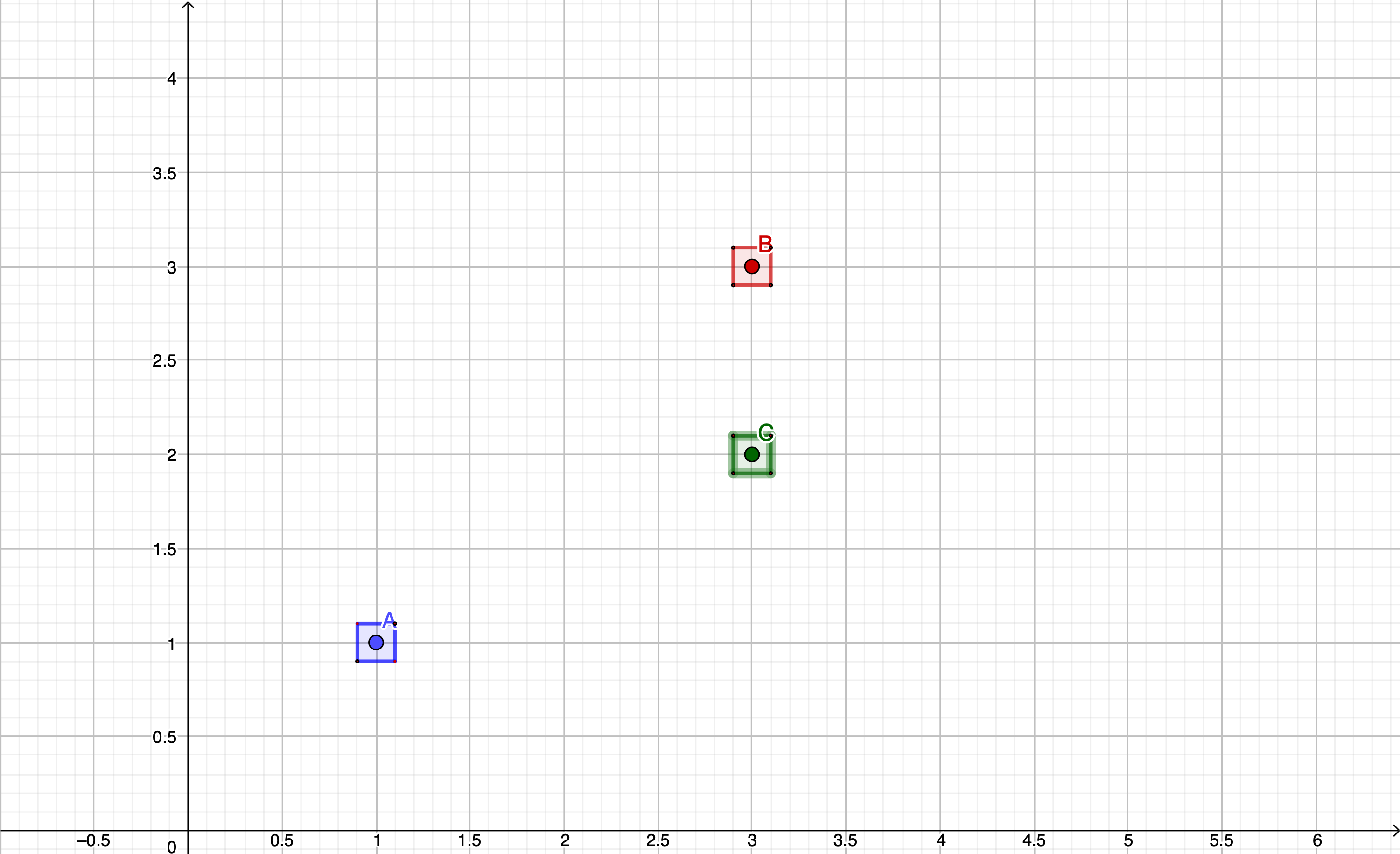
It takes an element with its bounding box minimum and maximum coordinates. As in our scenario, we are using points as locations we need to somehow translate them into bounding boxes that are being accepted by the GKRTree API. We can achieve that by simply adding some padding to their coordinates. We can do it by adding computed variables to the SomeLocation class.
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
...
var boundingBoxMin: vector_float2 {
vector_float2(x-boundingBoxSize, y-boundingBoxSize)
}
var boundingBoxMax: vector_float2 {
vector_float2(x+boundingBoxSize, y+boundingBoxSize)
}
}
The paddings we have just added can be now visualized on the diagram.
We can now add the elements to the tree
sampleLocations.forEach { location in
rTree.addElement(location,
boundingRectMin: location.boundingBoxMin,
boundingRectMax: location.boundingBoxMax,
splitStrategy: .reduceOverlap)
}
The last parameter used when adding elements is the splitStrategy. It defines how the tree reorganizes its internal structure. Four different strategies can be applied. The overall result depends on the organization of data you process, so it's valuable to check different strategies and compare the performance to pick the most efficient one.
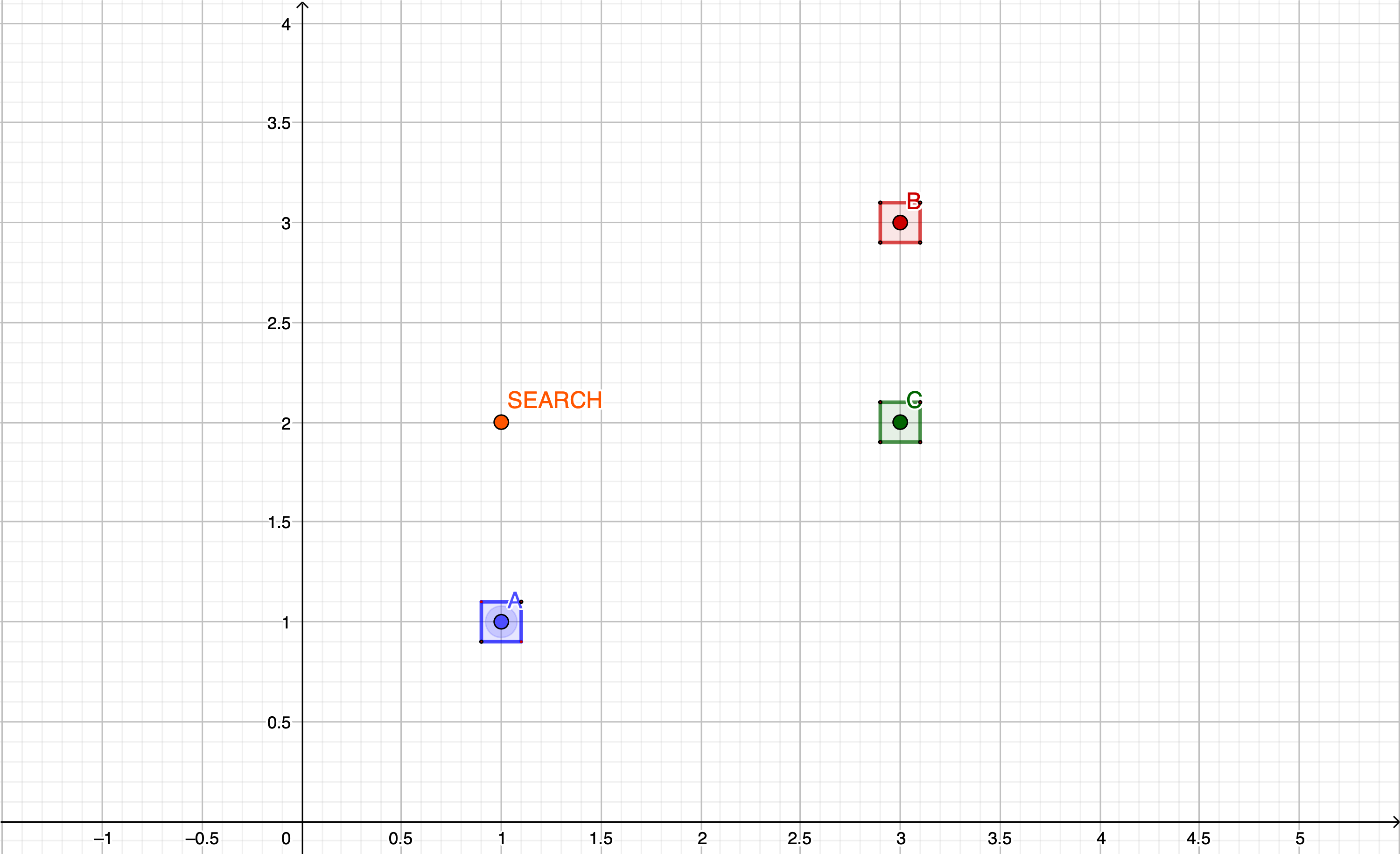
Now, it's time to search the closest neighbors for a selected point. Let's assume that it will be that it will be at (1,2). Looking at the GKRTree's search method we can see that it accepts, similarly to the one used for adding elements, bounding box boundaries.
func elements(inBoundingRectMin rectMin: vector_float2, rectMax: vector_float2) -> [ElementType]
That leads us to specify the area in which we want to find points.
let searchPosition = SomeLocation(name: "S", x: 1.0, y: 2.0)
let searchBoxSize: Float = 1.5
let searchBoxMin = vector_float2(searchPosition.x - searchBoxSize,
searchPosition.y - searchBoxSize)
let searchBoxMax = vector_float2(searchPosition.x + searchBoxSize,
searchPosition.y + searchBoxSize)
The search bounding box can be added to our diagram as well. As we can see below - we should expect getting one location back as there is only one element falling into the bounding box we just defined.
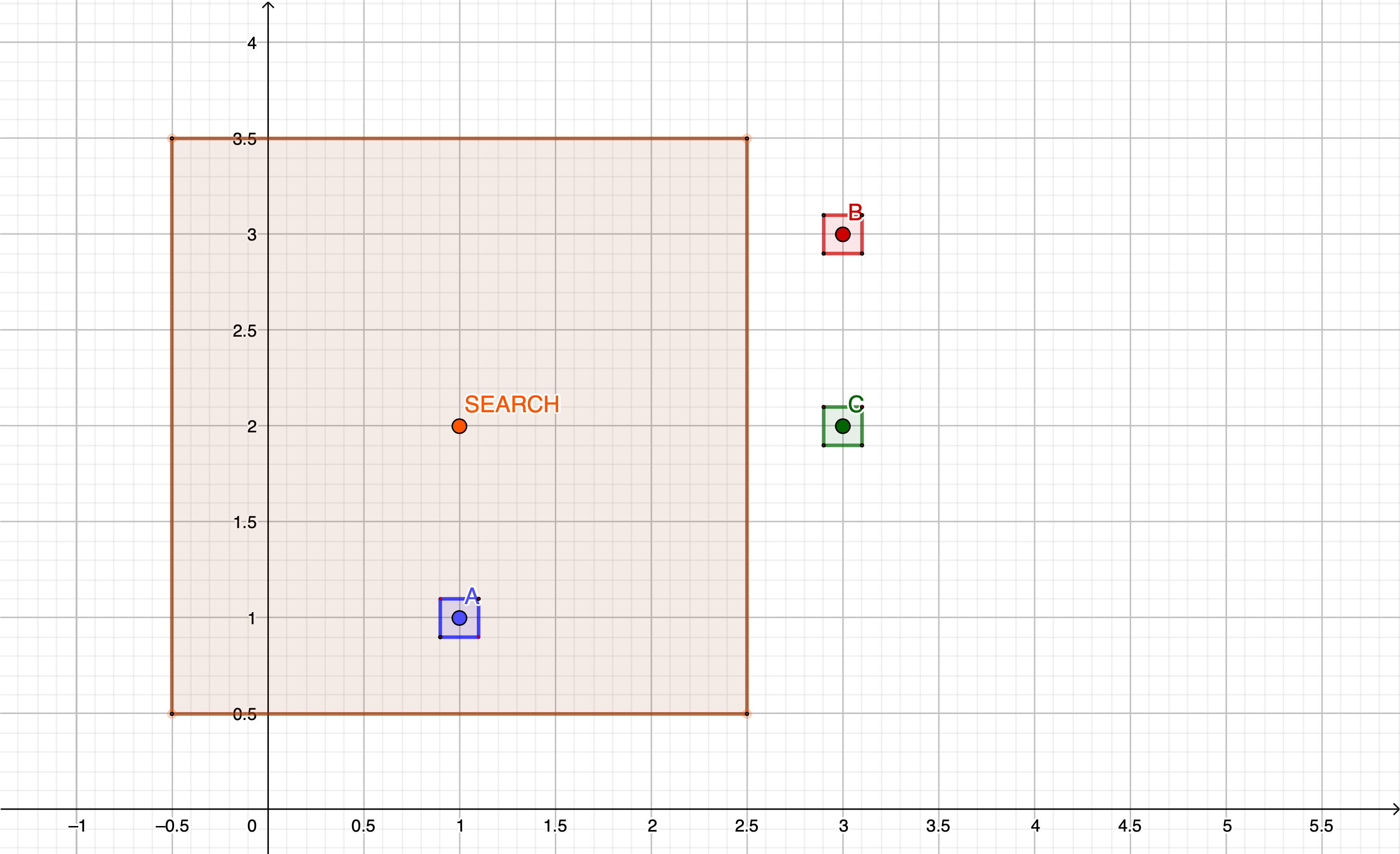
We can also observe that modifying the search criteria by increasing the box size gives us more results which can be later sorted, filtered and processed depending on the actual use case.
let results = rTree.elements(inBoundingRectMin: searchBoxMin, rectMax: searchBoxMax)
While using R-tree it's worth being aware that this data structure operates in a way that keeps the tree balanced. It means that no branch of the R-tree contains significantly more objects or sub-branches than any other branch. It results in increasing the amount of time required to perform insertion and deletion operations while decreasing the time needed to search for elements.
Complete example
The complete code for the discussed example looks as follows.
import GameKit
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
let name: String
let x: Float
let y: Float
init(name: String, x: Float, y: Float) {
self.name = name
self.x = x
self.y = y
super.init()
}
var boundingBoxMin: vector_float2 {
vector_float2(x-boundingBoxSize, y-boundingBoxSize)
}
var boundingBoxMax: vector_float2 {
vector_float2(x+boundingBoxSize, y+boundingBoxSize)
}
}
let sampleLocations = [
SomeLocation(name: "A", x: 1.0, y: 1.0),
SomeLocation(name: "B", x: 3.0, y: 3.0),
SomeLocation(name: "C", x: 3.0, y: 2.0)
]
let rTree = GKRTree(maxNumberOfChildren: sampleLocations.count)
sampleLocations.forEach { location in
rTree.addElement(location,
boundingRectMin: location.boundingBoxMin,
boundingRectMax: location.boundingBoxMax,
splitStrategy: .reduceOverlap)
}
let searchPosition = SomeLocation(name: "A", x: 1.0, y: 2.0)
let searchBoxSize: Float = 1.5
let searchBoxMin = vector_float2(searchPosition.x - searchBoxSize,
searchPosition.y - searchBoxSize)
let searchBoxMax = vector_float2(searchPosition.x + searchBoxSize,
searchPosition.y + searchBoxSize)
let results = rTree.elements(inBoundingRectMin: searchBoxMin, rectMax: searchBoxMax)
Wrap up
R-trees are a widely-applied data structure that may be used for implementing various sorts of spatial data searches. For Apple's platforms, there is a built-in implementation provided in the GameKit framework that makes implementing search on spatial data really quick. If you happen to need a 3D equivalent, be sure to check GKOctree. I hope that the presented example was a useful base for implementing your own solutions.
Thanks for reading!